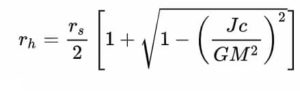A moins de vivre dans une galaxie très très lointaine, vous n’avez probablement pas du échapper aux milliers de publications, articles, posts Facebook ou tweets présentant la photographie du trou noir M87* et insistant sur sa dimension « historique ». Quelques explications sur cette image et sur les moyens mis en oeuvre pour la réaliser pour mieux comprendre en quoi elle est historique… à plus d’un titre !
Le 10 avril 2019 restera dans les mémoires comme la date à laquelle, pour la première fois, l’image d’un trou noir a été révélée.


En moins d’une journée, l’image a fait le tour du monde : divulguée lors de 6 conférences de presse simultanées organisées par les différents centres de recherche impliqués dans sa réalisation, cette image a été immédiatement relayée par tous les médias et partagée des millions de fois en quelques heures sur Internet… parfois presque jusqu’à la saturation !
Au cours de la journée du 10 avril, mon « mur » Facebook ne contenait ainsi plus qu’une longue succession de la même image, reprise en boucle, qui a même été détournée et parodiée le jour même.
Il est rare qu’une image « scientifique » accède immédiatement à une popularité aussi large, et plus encore s’inscrive de manière instantanée dans l’imaginaire collectif. Mais il ne s’agit pas de n’importe quelle image : il s’agit de l’image d’un trou noir !
Ces objets mythiques, qui découlent des équations de la théorie de la relativité générale formulée par Einstein en 1915, font partie de ces rares exemples de théories scientifiques qui frappent immédiatement l’imagination et qui demeurent – sur le principe – assez simples à concevoir pour que tout un chacun puisse se les représenter. La science-fiction s’est ainsi emparée de ces objets bien avant que leur existence ne soit confirmée par les observations : on ne compte plus les romans ou les films comportant une intrigue « tournant autour » d’un trou noir.

Si vous êtes amateur d’astronomie, il y a fort à parier que l’une de vos connaissances, informée de votre passion, vous a déjà posé une multitude de questions sur l’Univers… et que les trous noirs figuraient en bonne position (surtout depuis le film « Interstellar…). A titre personnel, j’ai à de nombreuses reprises été amené à discuter avec des néophytes en astronomie qui m’avouaient d’emblée « ne rien y connaître » mais malgré tout « être fascinés par les trous noirs« . J’ai parfois constaté que ces personnes connaissaient plus de choses sur ces objets lointains, mystérieux (et encore hypothétiques) que sur notre propre système solaire !
Rien d’étonnant cependant : les trous noirs sont des objets extrêmement attractifs… et pas seulement au niveau gravitationnel ! Ils absorbent tout, mais pas l’imagination : un énorme « trou » sans fond qui attire tout autour de lui, y compris la lumière, pour ne jamais rien laisser ressortir… Impossible de savoir ce qu’il contient, ni où il mène… Puits sans fond ou peut-être même un portail vers d’autres univers ou d’autres dimensions ? Abyssal, mystérieux, reflet de nos propres angoisses et de certains mythes ; donc forcément fascinant.
Mais « popularité » n’est pas synonyme de « compréhension », et bien souvent l’image que le grand public se fait d’un trou noir se limite à une représentation simpliste – et fausse – d’un « aspirateur cosmique ».
Nous allons tenter dans cet article de proposer une description assez rigoureuse (mais malgré tout vulgarisée) de ce que sont les trous noirs, afin de mieux prendre la mesure du caractère « historique » de l’image de M87*. Nous dirons également quelques mots de la technique utilisée pour réaliser cette image, au moins aussi historique que l’image elle-même !
1. Qu’est-ce qu’un trou noir ?
Les prémices : le concept « d’astre occlus » en mécanique Newtonienne
Le concept de trou noir n’est pas récent puisqu’il faut remonter au 18e siècle pour en trouver les premières « ébauches », alors désignées sous le terme « d’astre occlus ». A l’époque, ces concepts reposent sur la théorie universelle de la gravitation formulée par Isaac Newton en 1687, et sur le caractère fini de la vitesse de la lumière démontré pour la première fois par l’astronome danois Rømer en 1675 au moyen de l’observation des éclipses des satellites de Jupiter.
La théorie de la gravitation formulée par Newton implique que 2 corps massifs (A et B) s’attirent réciproquement par une « force » (F) dont l’intensité est proportionnelle à leurs masses (Ma et Mb), et inversement proportionnelle au carré de leur distance (d).
Autrement dit, plus les corps sont massifs, plus ils s’attirent.
Et cette force attractive diminue rapidement lorsque leur distance augmente.

Par exemple, posons que 2 corps situés à une distance de 1 s’attirent avec une force valant 1. A une distance de 2, la force attractive ne sera plus que de 1/4 ; et à une distance de 10, la force ne sera plus que de 1/100 ! Cette force est donc fortement décroissante avec la distance.
Gardons ce mécanisme général en tête, mais nous allons désormais raisonner « à la surface » d’un objet, ce qui va nous permettre d’éliminer le paramètre de distance et la décroissance de force qui l’accompagne.
Nous voici donc à la surface de la Terre, et pour les besoins de l’exercice, imaginons-nous tenir dans une main une balle de tennis : à quelle vitesse faut-il lancer cette balle à la verticale pour que celle-ci ne retombe pas ? Ou, autrement dit, que celle-ci échappe à la force gravitationnelle de la Terre ? Intuitivement, on se dit naturellement que plus un corps est massif, plus il sera difficile d’échapper à son attraction, et donc plus la vitesse de libération sera élevée…
Les équations de la théorie de Newton permettent de déterminer cette « vitesse de libération ». Dans la mesure où nous sommes situés à la surface de l’objet, cette vitesse de libération peut s’établir sous la forme ci-contre, avec M la masse du corps et R son rayon. Notre intuition initiale est donc confirmée : la masse de l’objet tient un rôle déterminant. Notons toutefois qu’il sera plus simple d’atteindre la vitesse de libération en augmentant la valeur de R, par exemple en tentant cet exercice depuis le sommet de l’Everest plutôt que depuis le niveau de la mer… à supposer bien sûr que vous ayez encore assez de souffle pour effectuer ce jet !
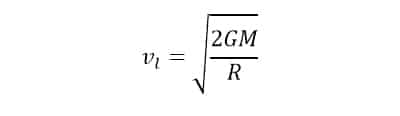
Le calcul permet d’établir que la vitesse de libération à la surface de la Terre est de 11,2 km/s. A ce stade, vous l’avez compris, inutile de continuer à essayer de lancer votre balle de tennis, cette expérience est vouée à l’échec… même si vous vous appelez Rafael Nadal et que vous disposez d’un bras gauche hypertrophié ! 🙂 Même à la surface de la Lune, pourtant bien moins massive que la Terre, la vitesse à atteindre reste respectable : 2,3 km/s. En revanche, si vous vous teniez à la surface de la comète Churyumov-Gerasimenko, la vitesse à atteindre ne serait que de 1m/s : largement de quoi décoller juste en faisant un petit bond (ou faire rebondir dans l’espace une sonde qui tenterait de s’y poser, par exemple) !
Mais que se passe t-il sur des corps plus massifs que la Terre ? Pas de suspens ici, la réponse est évidente : il faudra aller plus vite pour s’échapper : par exemple 60 km/s sur Jupiter ou 617 km/s à la surface du Soleil…
Le Soleil est le corps le plus massif du système solaire… mais nous pouvons effectuer cette expérience de pensée sur d’autres corps : des étoiles plus massives, un amas d’étoiles, une galaxie toute entière (1000 km/s pour la Voie Lactée)… et même sur des objets hypothétiques disposant d’une masse considérable et d’un diamètre limité. Des objets très « compacts », donc.
C’est à ce stade qu’intervient la découverte de la vitesse finie de la lumière, qui flirte avec les 300 000 km/s dans le vide. Si cette vitesse n’était pas encore établie avec une très grande précision au 18e siècle, le principe de base demeurait malgré tout valable : la lumière ne se propage pas instantanément, c’est à dire avec une vitesse infinie. Par ailleurs, la théorie de la lumière développée notamment par Newton, de nature corpusculaire, conduit à penser que la lumière a bien une masse, si faible soit-elle ; et donc qu’elle doit être soumise aux mêmes lois que les corps plus massifs.
Dès lors, il est possible d’imaginer qu’un objet soit suffisamment massif et compact pour que la vitesse de libération à sa surface soit supérieure à la vitesse de la lumière.
Que se passerait-il dans ce cas ?
La réponse est simple : la lumière qui serait émise à la surface d’un tel corps finirait inéluctablement par « retomber », de la même manière que la balle de tennis propulsée par nos petits bras chétifs dans l’expérience précédente !
« Il est possible que les plus grands corps lumineux de l’univers puissent être invisibles. »

Pierre-Simon de Laplace
Exposition du Système du Monde (1796)Par conséquent, l’astre en question n’émettrait aucune lumière et serait de ce fait « invisible ». Dans le système Newtonien, un « trou noir » est donc simplement un corps pour lequel la vitesse de libération est supérieure à la vitesse de la lumière.
C’est à cette conclusion que parviennent indépendamment l’anglais John Mitchell en 1783 et le français Pierre-Simon de Laplace en 1796. La renommée de ce dernier, et sa maîtrise de la mécanique céleste, donneront bien plus d’autorité à cette hypothèse que les travaux de Mitchell. Laplace formule ainsi cette hypothèse :
« Un astre lumineux, de la même densité que la Terre, et dont le diamètre serait 250 fois plus grand que le Soleil, ne permettrait, en vertu de son attraction, à aucun de ses rayons de parvenir jusqu’à nous. Il est dès lors possible que les plus grands corps lumineux de l’univers puissent, par cette cause, être invisibles. » (Pierre-Simon de Laplace, Exposition du Système du Monde ; 1796)
Malgré la grande autorité de Laplace, la présentation de cette théorie devant l’Académie des Sciences ne recueillera guère d’adhésion auprès de ses confrères. Il s’agit à leurs yeux d’un cas bien théorique et hautement improbable en l’état des connaissances de l’époque. Dans les années suivantes, la théorie « ondulatoire » de la lumière s’imposera (et avec elle l’absence de masse de la lumière), marquant un coup fatal à cette hypothèse, née sous une mauvaise étoile… Laplace finira même par supprimer cette référence à ce qu’il nomme les « astres occlus » dans la 3e édition de son ouvrage.
Il faudra attendre plus d’un siècle, et la théorie de la relativité générale, pour que le concept de trou noir refasse surface…
Une précision cependant…
Pour être vraiment précis, signalons tout de même un point important : contrairement à ce que nous venons d’exposer, la théorie Newtonienne ne permet pas d’expliquer le concept moderne de « trou noir » !
En effet, l’argument de la vitesse de libération permet de comprendre intuitivement le concept, mais n’est pas réellement pertinent, pour plusieurs raisons.
La première raison est que la vitesse de libération envisagée est celle qui doit être communiquée à un objet dès son départ de la surface, sans aucune force additionnelle par la suite. Mais en pratique, il est tout à fait possible d’imaginer qu’on communique à un corps une accélération moindre, lui donnant une vitesse inférieure à la vitesse de libération, mais qui soit continue. Il faudra certes une grande quantité d’énergie pour compenser à tout instant l’effet de la gravité, mais cela reste théoriquement possible. Donc, moyennant une grande quantité d’énergie, il est possible en théorie Newtonienne de faire échapper un corps de l’attraction gravitationnelle d’un autre en lui donnant une vitesse bien inférieure à la vitesse de libération !
Un exemple quotidien est celui des sondes que nous envoyons dans l’espace : aucune fusée n’atteint la vitesse de 11km/s ! La plus puissante fusée jamais construite, la Saturn V qui servit à envoyer les missions Apollo sur la Lune, ne dépassait pas les 9600 km/h à la fin de la combustion du premier étage… soit « juste » 2,66 km/s ! Une fois en orbite, la vitesse de libération diminue ; elle n’est plus par exemple que de 4 km/s pour une sonde en orbite à 36000 km d’altitude, vitesse qu’il est facile d’atteindre en lui communiquant une accélération au moyen d’un moteur de poussée intermédiaire.
La seconde raison, plus fondamentale, est qu’à l’époque de Newton, on sait déjà que la vitesse de la lumière est finie, mais pas qu’il s’agit d’une vitesse limite infranchissable. Il restait donc toujours possible en théorie de dépasser cette vitesse au moyen d’une énergie importante, y compris pour un corps massif !
Les trous noirs : une conséquence de la relativité générale
Albert Einstein publie en 1915 la théorie de la relativité générale, qui bouleverse profondément notre conception de l’espace, du temps et de la gravitation… et dont les trous noirs sont une des conséquences directes.
Il est bien sûr impossible d’entrer dans le détail de cette théorie, aussi nous présenterons uniquement les principes fondamentaux qui sont indispensables à une bonne compréhension de ce que sont les trous noirs.

Contrairement à la mécanique Newtonienne, où l’espace et le temps sont des entités absolues et indépendantes de la matière ; la relativité générale pose le principe de l’existence d’un concept d' »espace-temps » étroitement lié à la matière qu’il contient.
Cette conception est révolutionnaire : un peu comme si la scène d’un théâtre devenait subitement l’un des protagonistes de la pièce qui se jouait jusqu’ici autour d’elle !
La notion de « temps » n’est plus absolue non plus, mais est désormais liée à la structure de l’espace-temps : l’écoulement du temps n’est pas le même selon le référentiel envisagé. Ainsi, les horloges de deux observateurs, l’un immobile et l’autre en mouvement accéléré, ne s’écouleront pas à la même vitesse du point de vue de chacun des observateur. Bien que cet aspect implique des conséquences fascinantes, nous ne rentrerons pas davantage dans le détail ici car il n’est pas indispensable à la compréhension des trous noirs…
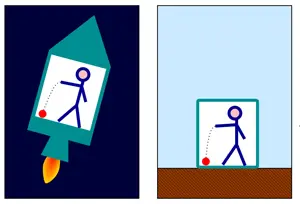
Einstein établit également un concept fondamental, celui « d’équivalence » entre la gravitation et l’accélération, qui ne sont plus que deux aspects d’un même phénomène. Techniquement, cela revient à poser l’équivalence entre la masse pesante (qui détermine le poids d’un corps dans un champ de gravité) et la masse inertielle (la résistance d’un corps à une accélération).
Pour illustrer simplement cette « équivalence », on utilise souvent cette représentation : il n’existe aucune expérience physique permettant de déterminer, pour une personne enfermée dans une cabine hermétique, si elle est simplement posée à la surface de la Terre ou embarquée dans une fusée dotée d’une accélération constante reproduisant l’accélération de la gravité terrestre. De la même manière, l’expérience sera identique dans le cas d’un ascenseur en chute libre sur Terre ou dans une cabine flottant dans l’espace loin de toute source de gravité (apesanteur) : pendant sa chute, la personne dans l’ascenseur « flottera » librement, ainsi que tous les objets présents dans la cabine, comme s’ils n’étaient soumis à aucune force gravitationnelle.
C’est là l’idée de génie d’Einstein : la gravitation ne s’envisage plus comme une force, mais comme la trajectoire naturelle, en chute libre, d’objets situés dans un espace-temps « courbé ».
Cette théorie permet de répondre de manière très élégante à plusieurs questions fondamentales qui demeuraient en suspens dans la théorie de Newton : quelle est la nature de la « force » de gravitation entre les objets massifs, quelle est l’origine de cette force et sous quelle forme se propage t-elle ?
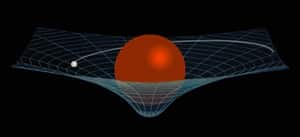
Dans le modèle d’Einstein, ces questions n’ont plus lieu d’être… car il n’existe en réalité aucune « force » : la matière déforme l’espace-temps, et l’espace-temps dicte en retour à la matière comment elle doit se comporter dans cet espace déformé. Ainsi, les objets massifs déforment l’espace-temps, et les objets présents dans cet espace-temps déformé suivent des « lignes droites », ou plutôt des géodésiques », régies par la géométrie de l’espace-temps. Autrement dit, la Terre ne « tourne » pas autour du Soleil, comme retenue par un fil invisible (une « force »), mais se contente d’être en « chute libre » dans un espace-temps déformé par le Soleil ; sa trajectoire se traduisant par une rotation autour de l’objet massif central.
Autre point fondamental (déjà à la base de la relativité restreinte énoncée par Einstein en 1905) : la vitesse de la lumière dans le vide (« c ») est la vitesse maximum à laquelle un objet peut se déplacer dans l’espace-temps. La lumière étant dépourvue de masse, cette vitesse est même inatteignable par tout corps massif puisque la moindre masse impliquerait une énergie infinie pour l’accélérer jusqu’à c ; en application (un peu modifiée) de la célébrissime formule E = mc². Les objets dotés d’une masse, tels que les particules élémentaires, peuvent donc avoir des vitesses « relativistes » (proches de c), mais ne peuvent jamais atteindre la vitesse de la lumière… et encore moins la dépasser. Autre aspect essentiel (dont nous allons passer sous silence les implications fondamentales…) : la lumière se propage dans le vide à une vitesse « c » constante quelque soit le référentiel d’observation !
La vitesse de la lumière « c » est ainsi la vitesse maximale à laquelle toute information peut être communiquée au sein de l’espace-temps ; ce qui vaut aussi pour la déformation de l’espace-temps imprimée par les objets qui y sont présents. Alors que Newton pensait que la force de gravité se propageait de manière instantanée, Einstein vient limiter cette propagation d’information à la vitesse de la lumière : la déformation de l’espace-temps s’effectue à cette vitesse. Ainsi, si le Soleil disparaissait brusquement, la Terre ne quitterait son orbite pour poursuivre sa route en ligne droite que 8 minutes plus tard… en même temps que sa lumière s’éteindrait pour nous soudainement.
Bien sûr, nous n’avons fait ici que survoler très rapidement quelques uns des principes essentiels qui permettent de comprendre les implications physiques de la théorie de la relativité générale. Mais nous avons fait abstraction d’un élément essentiel dont il convient de dire un mot à défaut d’envisager de l’exposer en détails : cette théorie repose sur des outils mathématiques extrêmement complexes (les tenseurs notamment) et fait appel à des outils géométriques innovants, non-euclidiens.

Jusqu’ici, la géométrie de l’Univers n’était envisagée que sous sa version euclidienne ; qui implique entre autres postulats que 2 droites parallèles ne se croisent jamais. Dans un univers à géométrie « plane », cela semble aller de soi, c’est pourquoi il est impossible de dessiner sur une feuille de papier un triangle dont la somme des angles n’est pas égale à 180°.
Le célèbre mathématicien Carl Friederich Gauss avait déjà, au début du 19e siècle, développé des outils géométriques non-euclidiens, c’est à dire destinés à décrire des espaces présentant une courbure non nulle (espace non plat). Dans ce cadre, il est possible d’imaginer des espaces dotés d’une infinité de valeurs de courbure différentes, dont la valeur 0, qui correspond à la géométrie euclidienne, n’est plus qu’un cas très particulier. Viennent ainsi s’ajouter à la géométrie euclidienne les géométries à courbure négative (où la somme des angles d’un triangle est inférieure à 180°) et des géométries à courbure positive (où la somme des angles d’un triangle est supérieure à 180°).
Pour traduire sa nouvelle conception de la gravitation et d’un espace-temps déformé, Einstein va utiliser la géométrie développée quelques années auparavant par le mathématicien Bernhard Riemann. Cette géométrie permet de décrire des espaces dotés d’une courbure, sans pour autant nécessiter de faire appel à des dimensions supplémentaires.
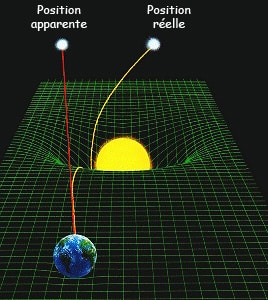
Dans de tels espaces, dotés d’une courbure, le plus court chemin entre deux points n’est plus nécessairement la ligne droite, mais une géodésique : exactement ce qu’il faut à Einstein pour décrire le mouvement en chute libre des corps dans un champ de gravitation résultant de la déformation de l’espace-temps !
Nous y reviendrons plus tard, mais notons qu’une telle courbure provoque des « mirages » lumineux à proximité des corps massifs, comme l’illustre l’image ci-contre…
Einstein va ainsi formaliser la relation existant entre la quantité de matière et la courbure de l’espace-temps en résultant. La « métrique » de l’espace-temps (exprimant la courbure) est ainsi reliée à la matière, exprimée sous forme de masse et d’énergie.
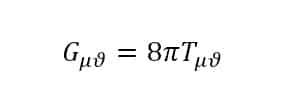
Dans sa version très simplifiée ci-contre, voici « l’équation d’Einstein », qui est au centre de la formalisation mathématique de la théorie de la relativité générale. Il n’est pas nécessaire de comprendre dans le détail les subtilités de cette équation, mais retenons que l’expression de gauche (G) décrit la courbure de l’espace-temps, et l’expression de droite (T) le contenu « masse-énergie » de l’espace-temps.
Avec cette formule, il est donc possible de décrire précisément comment l’espace-temps est déformé par la matière. L’utilisation de la géométrie riemannienne permet de décrire en retour comment la matière se comporte au sein de cet espace-temps déformé (géodésiques).

Mais la simplicité de cette équation n’est qu’apparente, car les deux aspects s’influencent réciproquement et la solution complète est en réalité décrite par 10 équations hautement non-linéaires ! Einstein lui-même, lors de la publication de cette formule, doutait de la possibilité de trouver des solutions analytiques exactes…
Pourtant, il ne faudra que quelques mois à Karl Schwarzschild, un astrophysicien de génie alors mobilisé sur le front russe, pour trouver une solution à cette équation décrivant le champ gravitationnel résultant d’une quantité de matière concentrée en un point et sans rotation. Cette solution implique une hypothèse de départ très « simplifiée » (mais qui peut être généralisée assez facilement) et qui va voir resurgir le concept de « trou noir ».
La métrique de Schwarzschild décrit ainsi le champ gravitationnel, ou la déformation de l’espace-temps, induite par une masse sphérique.

Dans la représentation ci-contre, on voit que plus on s’éloigne de la masse centrale, plus la déformation de l’espace-temps est faible. Si l’on s’en éloigne suffisamment, la métrique de l’espace-temps redevient sans courbure, et les solutions de la mécanique Newtonienne s’appliquent parfaitement.
Mais les choses sont plus complexes dès lors que l’on s’approche du centre de l’objet massif… Au centre de celui-ci, le champ gravitationnel et la courbure de l’espace-temps tendent vers l’infini. Or, les théories physiques s’accommodent mal de la notion « d’infini » qui peut résulter de la mise en oeuvre d’équations mathématiques ; souvent synonyme d’une imperfection du modèle qui n’est plus à même de décrire la réalité physique des objets dans des conditions limites. On parle alors de « singularité ».
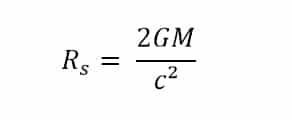
Schwarzschild démontre même qu’il n’est pas nécessaire d’atteindre le centre de l’objet pour que les équations d’Einstein « ne fonctionnent plus » (c’est à dire donnent des valeurs incohérentes physiquement) : il démontre qu’il existe également une seconde singularité située à une certaine distance au centre, en deçà de laquelle sa métrique ne donne plus de résultats cohérents. Cette distance « limite », que l’on appelle « rayon de Schwarzschild » est définie uniquement par la masse de l’objet et se calcule au moyen de l’équation ci-contre (où M est la masse de l’objet, G la constante de gravitation et c la vitesse de la lumière).
Techniquement, en deçà de ce rayon, la courbure de l’espace-temps est tellement forte que la trajectoire de la lumière prend la forme d’une ellipse : condamnée à tourner indéfiniment autour du point central à l’image de la Terre autour du Soleil… et donc à ne plus s’échapper. Et voilà le concept de « trou noir » qui refait surface !
Cette valeur « limite » est tout d’abord intuitivement perçue, par Schwarzschild comme par Einstein, comme une singularité dépourvue de sens physique. Toutefois, ce rayon limite étant très inférieur au rayon d’une étoile, cela n’empêche pas d’utiliser la métrique de Schwarzschild pour décrire le champ de gravitation de celle-ci… Le calcul montre par exemple que le rayon de Schwarzschild pour une étoile telle que le Soleil est d’à peine 3 kilomètres, et de quelques millimètres seulement pour un corps aussi massif que la Terre. Ces phénomènes ne sont donc pas perceptibles sur les objets que l’on observe habituellement et les calculs réalisés pour le système solaire, par exemple, n’en sont pas affectés.
A ce stade, les bases physiques et mathématiques essentielles à la conceptualisation du trou noir sont posées… il reste toutefois à surmonter l’obstacle « psychologique » et théorique de la « compacité » de tels objets…
Troublants trous noirs…
N’y a t-il réellement aucune signification physique à la singularité découverte par Schwarzschild ? Difficile de critiquer la première intuition d’Einstein : imaginez toutes les montagnes, les océans, l’atmosphère, les déserts, l’intérieur de la Terre y compris son noyau de fer comprimés dans le volume d’un dé à coudre ! Inimaginable à l’époque, où les objets les plus compacts connus sont extrêmement éloignés – de plusieurs ordres de grandeur – de ces valeurs colossales de densité !
Cependant, il faut souligner qu’un tel « problème » de densité – en dehors de la singularité centrale – ne se pose que pour les trous noirs peu massifs et donc pour lesquels le rayon de Schwarzschild est très petit. Mais si l’on imagine qu’il puisse exister des trous noirs extrêmement massifs, on peut démontrer que leur densité, au rayon de Schwarzschild, est au contraire très faible ; par exemple inférieure à l’atmosphère terrestre pour un trou noir de plusieurs milliards de masses solaires. Mais cela ne résout évidemment pas l’interrogation pour ce qui concerne la singularité centrale.

Il faudra attendre le début des années 1930 pour que la mauvaise intuition d’Einstein soit battue en brèche et qu’il soit admis que la limite de Schwarzschild n’est pas impénétrable, et donc qu’un astre puisse effectivement s’effondrer sur lui-même sous ce rayon « limite ». En quelques années, les travaux de brillants théoriciens rendent crédibles de tels objets à la densité extrême.
L’astrophysicien indien Subrahmanyan Chandrasekhar démontre ainsi en 1929 qu’au-delà d’une certaine masse (1,44 masse solaire), un objet doit s’effondrer sur lui-même sous l’effet de sa propre force de gravité, dès lors qu’aucune autre force ne vient contrarier cet effondrement. C’est le cas par exemple des naines blanches, étoiles en fin de vie dont les réaction de fusion nucléaire ont cessées.
C’est également le cas des étoiles à neutron, résidus de supernova dont la matière est condensée sous une forme « dégénérée » et extrêmement compacte, typiquement la masse du Soleil condensée en un astre de 20 kilomètres de diamètre…

Les physiciens Fritz Zwicky, Robert Oppenheimer et Hartland Snyder démontreront ensuite qu’il existe également une masse limite pour ces étoiles à neutrons (un peu moins de 3 masses solaire), au-dessus de laquelle celle-ci s’effondre inéluctablement sous sa propre gravité.
Par ailleurs, l’astrophysicien (et abbé) belge Georges Lemaître démontrera, en 1932, que la « limite de Schwarzschild » ne correspond pas à une réalité physique, mais résulte uniquement du choix des coordonnées utilisées pour le calcul de la métrique de l’espace-temps. Autrement dit, le choix d’un système de coordonnées plus adapté permet de faire disparaître la « singularité » de Schwarzschild des résultats de l’équation d’Einstein, et confère au « rayon de Schwarzschild » une réalité physique bien différente : celle d’un « horizon » au-delà duquel la courbure de l’espace-temps est si prononcée qu’elle interdit à tout objet y ayant pénétré d’en ressortir, ce dernier étant inéluctablement condamné à rejoindre la singularité centrale.
Avec ces découvertes, les bases théoriques sont désormais suffisantes pour approfondir l’étude physique de ces objets mystérieux… et de vérifier leur existence !
Pourtant, Einstein et d’autres éminents astrophysiciens (dont Arthur Eddington), s’obstineront malgré tout dans leur refus d’admettre ces nouvelles avancées théoriques importantes ; essentiellement en raison du trop grand décalage entre ces résultats et les objets alors connus et dont l’existence est avérée par l’observation à l’époque.
C’est ainsi que, ironiquement, le père de la relativité générale refusera lui-même de croire, pendant toute sa vie, en l’existence des trous noirs… objets issus de ses propres équations !
« Je pense qu’il doit exister une loi de la nature qui empêche une étoile de se comporter de façon aussi absurde. »

Arthur Eddington
(1935)« La « singularité de Schwarzschild » n’existe pas pour la raison que la matière ne peut être concentrée arbitrairement. »

Albert Einstein
(1939)Les développements rapides de la relativité générale dans les années 1960, après sa mort, confirmeront cependant la pertinence de cette théorie, et permettront véritablement aux trous noirs d’entrer dans le « bestiaire » officiel des objets astrophysiques.
Avec les avancées théoriques apportées dans les années 1930 par des chercheurs de premier plan tels que Chandrasekhar, Oppenheimer ou Zwicky, l’idée qu’il puisse exister dans l’Univers des astres beaucoup plus denses que les objets habituellement observés avait commencé à faire son chemin.
Mais la possibilité que des objets particuliers puissent exister théoriquement ne signifie pas que ceux-ci existent réellement… encore faut-il les observer ! Et si, sur le papier, il est possible de déterminer des masses « critiques » conduisant à l’effondrement des astres sur eux-mêmes, rien ne dit que de telles masses puissent être atteintes dans l’Univers.
Les découvertes réalisées dans les années 1960 vont cependant venir confirmer l’existence de ces astres « compacts ». Les naines blanches, déjà connues, sont découvertes par dizaines au cours des années 50 et 60 et de mieux en mieux étudiées. Mieux encore, les étoiles à neutrons, dont l’existence avait été envisagée dès la découverte du neutron par James Chadwick en 1932, et modélisées par raffinements successifs par Lev Landau, Zwicky, Oppenheimer et Snyder, sont confirmées en 1967 avec l’observation par Jocelyn Bell et Antony Hewish du premier « pulsar ».

Un pulsar (diminutif de « pulsating star« , étoile pulsante) est le résidu de l’explosion cataclysmique d’une étoile en supernova : une étoile à neutrons, un astre extrêmement dense et compact, tournant sur lui-même à des vitesses considérables (jusqu’à plus de 1000 tours par seconde !). En réalité, un pulsar n’a d' »étoile » que le nom, car il ne s’y produit plus aucune réaction nucléaire, et est uniquement composé de matière dans un état dit « dégénéré », produisant un champ électromagnétique intense. Lorsque la Terre est dans l’axe du champ magnétique, il est possible de détecter des « pulsations » extrêmement régulières, produites au rythme du nombre de rotations sur lui-même de l’astre.
Signe de la difficulté d’admettre alors encore la réalité physique de tels objets : lors de la découverte du premier pulsar, la régularité des pulsations était tellement précise qu’il fût d’abord envisagé que l’origine de ces signaux soit de nature… intelligente ! Il semblait a priori plus crédible qu’une vie extraterrestre puisse être à l’origine de tels signaux parfaitement réguliers plutôt que ceux-ci résultent d’un phénomène naturel. Cette hypothèse fût toutefois rapidement écartée par Hewish, à défaut de modifications du signal qui auraient caractérisé que ce signal soit émis depuis une planète en orbite autour de l’étoile…
L’existence d’objets aussi massifs que les étoiles à neutrons était désormais confirmée par la découverte des pulsars… mais les « trous noirs », encore plus compacts, demeuraient encore purement théoriques !
Une étape fondamentale va être franchie en 1963 grâce au mathématicien Roy Kerr, qui parvient à résoudre l’équation d’Einstein pour un trou noir en rotation. Cette solution implique notamment que la singularité centrale du trou noir n’est plus ponctuelle (comme dans la solution de Schwarzschild, mais annulaire. Dans la métrique de Kerr, les caractéristiques d’un trou noir peuvent être décrites uniquement à partir de sa masse M et de son moment cinétique J. Dans ce cas, le rayon de l’horizon des événements est au maximum égal à celui de Schwarzschild (pour un trou noir sans rotation qui ne devient qu’un cas particulier) et la moitié de cette valeur pour un moment angulaire maximum.
Cette solution sera même améliorée dès 1965 par Newman, qui généralise la solution de Kerr aux trous noirs en rotation et disposant d’une charge électrique non nulle.
A ce stade, la théorie des trous noirs est déjà considérablement développée… le terme « trou noir » est d’ailleurs employé pour la première fois en 1964 par le physicien américain John Wheeler, et s’impose rapidement comme une évidence dans le monde entier. Il ne reste plus qu’à en détecter un !
« Les trous noirs sont une source d’illumination »

John Wheeler
(1911 – 2008)Cette découverte sera finalement réalisée de manière concomitante, puisqu’en 1965 est observée une intense source de rayonnement X, Cygnus X-1, qui va fournir la première piste sérieuse de la détection d’un trou noir.
Des observations révèlent ainsi qu’une étoile supergéante, a priori banale, est en réalité en orbite autour d’une source intense de rayons X… sans qu’il soit cependant possible de détecter la moindre étoile compagnon ou le moindre objet à proximité qui serait susceptible d’être la source d’un tel rayonnement !

Les modélisations montrent que cette émission de rayons X suppose que l’étoile soit en orbite autour d’un objet massif, qui arrache une partie de son atmosphère : l’étoile elle-même ne pouvant être la source de ce rayonnement. Les recherches ultérieures démontrent que l’objet compagnon doit avoir une masse avoisinant les 10 masses solaires, ce qui exclut dès lors la possibilité d’une étoile à neutron (qui comme nous l’avons vu, doit s’effondrer sous sa propre gravité au-delà de 3 masses solaires).
En 1971, il est donc envisagé que cette mystérieuse source X soit en réalité un trou noir… faisant ainsi de Cygus X-1 le premier « candidat trou noir » clairement identifié de l’histoire de l’astrophysique !
Ces objets fascinants, qui n’existaient jusqu’ici que sur le papier, faisaient ainsi leur entrée dans le « bestiaire » cosmique… pour ne plus jamais en sortir.
2. Comment représenter un trou noir ?
Dés lors que de tels objets sont prédits par la théorie, mais également plausibles en tant d’objets physiques, se pose la question de la manière de se représenter un « trou noir » de manière cohérente avec le cadre de la relativité générale.
Pour ceux qui auraient sauté la première partie, voici un récapitulatif des bases théoriques de la théorie de la relativité générale, sur laquelle repose la représentation moderne des trous noirs :
- La relativité générale repose sur le concept d’espace-temps, représentation mathématique du « tissu » de l’Univers ;
- Les objets massifs déforment l’espace-temps, lui imprimant une courbure qui influence en retour les trajectoires des corps ;
- Contrairement à la théorie de Newton, la relativité générale ne décrit plus la gravitation comme une force mais comme la conséquence de la déformation de l’espace-temps par les corps massifs, les objets présents dans le champ de gravité étant en chute libre et leur trajectoire prend la forme de géodésiques, plus court chemin entre 2 points dans cet espace courbé ;
- La lumière se déplace à une vitesse « c » constante quelque soit le référentiel d’observation, et constitue la vitesse maximum qu’il est possible d’atteindre pour un corps dans l’espace-temps ;
- Les déformations de l’espace-temps – et donc la gravité – se propagent à la vitesse de la lumière ;
- Pour tout corps massif, il existe un rayon Rs en-deçà duquel la courbure de l’espace-temps est tellement forte que celui-ci se « replie sur lui-même » et qu’aucune information, pas même la lumière, ne peut en sortir : on parle « d’horizon des événements ».
Avant de se représenter un trou noir, il faut déjà essayer de conceptualiser ce qu’est l’espace-temps. Il est en effet compliqué de se représenter un corps à 3 dimensions dans un espace-temps à 4 dimensions…
Pour simplifier, utilisons l’analogie classique d’un drap tendu à plat sur lequel on poserait des boules de différentes masses.
La boule la plus lourde va déformer le drap et lui imprimer une courbure plus prononcée que les balles plus légères, dont le mouvement sera alors influencé par cette déformation.
Les trajectoires des balles légères vont prendre la forme de géodésiques et être soit déviées au passage de la boule la plus lourde, soit se transformer en ellipses autour de celle-ci. Cet exemple est très bien illustré par la vidéo ci-contre.
Bien sûr, l’analogie a ses limites… en particulier l’espace-temps est ici représenté en 2 dimensions et non en 4… mais remplacez mentalement les balles par des étoiles ou des planètes, et le drap par l’espace-temps, et vous aurez ainsi une bonne représentation de la nature de la gravitation dans la théorie de la relativité générale et la manière dont la masse déforme l’espace-temps !
Voyons maintenant comment cette représentation peut nous aider à appréhender la déformation de l’espace-temps par des objets de masses différentes.
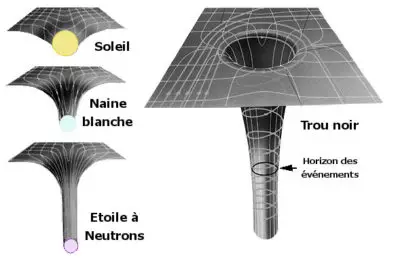
L’image ci-contre représente schématiquement la manière dont l’espace-temps est déformé par une étoile banale (le soleil), une étoile compacte en fin de vie (une naine blanche), un résidu de supernova très dense (une étoile à neutron), et un objet encore plus massif, un « trou noir ».
Pour ce dernier, la déformation de l’espace-temps est tellement importante qu’il n’est pas possible de représenter le « fond » du puits ainsi formé : celui-ci représente la « singularité centrale ». Il est toutefois possible de représenter l’horizon des événements, une frontière immatérielle qui délimite la zone de l’espace-temps au-delà de laquelle la vitesse de libération devient supérieure à la vitesse de la lumière : toute particule franchissant cet « horizon » sera inéluctablement entraînée vers la singularité centrale, sans aucune possibilité de retour en arrière.
A ce stade, plusieurs précisions importantes sont nécessaires.
1. L’horizon des événements n’a aucune matérialisation physique : il s’agit d’une frontière purement mathématique liée à la géométrie de l’espace-temps, dont la distance au centre du trou noir est déterminée uniquement par la masse totale de celui-ci. Il s’agit du « rayon de Schwarzschild » dont nous avons vu qu’il ne constitue pas une singularité si l’on retient des systèmes de coordonnées adaptés, notamment ceux de Lemaître.
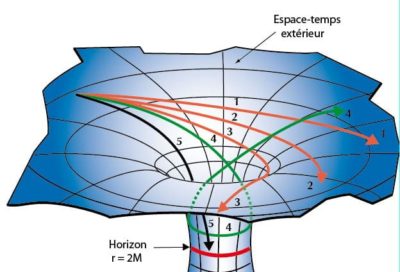
2. L’argument de la valeur de libération est ici valable, mais il est plus juste de dire que l’horizon délimite la zone de l’espace-temps où la courbure est tellement forte que les corps qui y entrent ne peuvent plus y prendre – au mieux – que des trajectoires elliptiques, et donc fermées : aucune géodésique n’existe qui leur permettrait de ressortir de cette zone. L’espace-temps est tellement courbé qu’il est comme « replié sur lui-même », se transformant en prison dont il n’existe plus aucune issue… En conséquence, une particule qui franchit cette limite ne pourra plus avoir une influence future à l’extérieur : c’est pourquoi on parle d’horizon « des événements ». Tout ce qui entre dans le trou noir ne peut plus avoir de contact ni d’influence avec les objets en dehors du trou noir.
3. Sur l’horizon, les orbites des photons sont parfaitement circulaires, et la moindre déviation conduit à les faire tomber dans le trou noir. Plus une particule se rapproche de l’horizon, plus la marge de manœuvre est petite pour qu’elle puisse s’échapper, la vitesse de libération tendant vers la vitesse de la lumière : c’est pourquoi les orbites sont de plus en plus « instables » à l’approche de l’horizon.
4. Dans la mesure où tout élément franchissant l’horizon des événements ne peut plus ressortir, la masse totale d’un trou noir ne peut qu’augmenter avec le temps (ou demeurer constante si aucune particule massive ne croise jamais sa route…). Stephen Hawking a cependant démontré en 1975 qu’un infime rayonnement de corps noir au niveau de l’horizon des événements devrait conduire à une « évaporation » d’un trou noir… mais au bout d’une durée plusieurs milliards de fois supérieure à l’âge de l’Univers !
5. La valeur du rayon de l’horizon est déterminé uniquement par la masse du trou noir. En conséquence, un trou noir de masse « faible » (quelques masses solaires) aura un horizon de très petite dimension (3km par exemple dans le cas d’une masse solaire). Il s’agira donc d’un objet extraordinairement dense. Mais pour un trou noir disposant d’une masse de plusieurs millions, voire milliards de masses solaires, cet horizon pourra être repoussé à plusieurs dizaines de milliards de kilomètres du centre de la singularité centrale… Un tel trou noir « supermassif », s’il est très compact, est cependant très peu dense (au sens de la masse volumique) et peut même présenter une densité inférieure à celle de l’atmosphère terrestre !
6. A mesure que l’on se rapproche du trou noir, certains phénomènes étranges font leur apparition. Les effets relativistes sont ici pleinement à l’oeuvre et les équations d’Einstein commencent à tendre vers des valeurs « limites ». Ces phénomènes sont multiples, mais sont tous dus à la proximité du champ de gravité intense (ou, ce qui revient au même, à la courbure extrême de l’espace-temps).
- De forts effets de marée : de la même manière que la Lune déforme un peu plus la surface de la Terre orientée vers elle que celle qui lui est opposée, ce qui occasionne le phénomène des marées océaniques, un trou noir va engendre des effets de marées similaires dans leur principe… mais pas dans les mêmes proportions ! En effet, l’intensité du champ gravitationnel va conduire à des différences de vitesse de chute très différentes sur de très courtes distances, conduisant à un étirement puis une dislocation de n’importe quel corps au niveau de la singularité centrale. A noter que cet effet n’est pas lié à l’horizon lui-même : ces effets de marée intenses seront perceptibles bien avant d’arriver au niveau de l’horizon pour un trou noir massif ; et au contraire il serait possible de franchir l’horizon sans ressentir le moindre effet de marée pour un trou noir supermassif.
- Un « rougissement » de la lumière : de la même manière que la lumière d’un objet s’éloignant de l’observateur apparaît « décalée vers le rouge », un champ de gravité intense va « dilater » les longueurs d’onde de la lumière. Ainsi, plus la lumière passera près de l’horizon des événements, plus sa longueur d’onde sera étirée, rendant celle-ci plus rouge et plus faible en intensité, jusqu’à disparaître totalement dans des longueurs d’onde hors du spectre visible… Dans le cas d’un trou noir en rotation doté d’un disque d’accrétion, la matière s’éloignant de nous sera fortement atténuée et rougie, tandis que la matière s’approchant de nous sera fortement renforcée et bleuie.
- Des « mirages gravitationnels » : à proximité du trou noir, la courbure de l’espace temps est tellement forte que la trajectoire de la lumière se trouve fortement déviée : les rayons lumineux passant au plus près peuvent effectuer un demi-tour et repartir dans leur direction d’origine, voire même réaliser plusieurs tours du trou noir avant de repartir dans une autre direction !
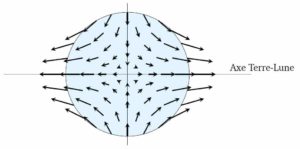
Représentation des effets de marée.
Crédit : Frédéric Chambat – ENS Lyon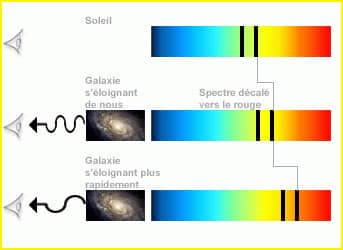
Représentation de l’effet Doppler et du décalage des raies spectrales vers le rouge. Crédit : Observatoire de Paris 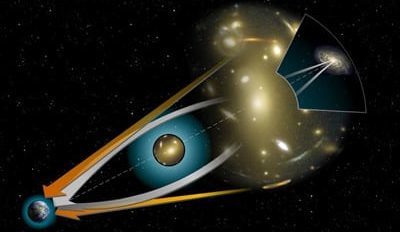
« Mirages gravitationnels » provoqués par la présence d’un objet massif entre la source et l’observateur.
- Une dilatation du temps : nous avons évoqué précédemment que, dans la théorie de la relativité restreinte, le temps ne s’écoule pas de la même manière pour deux observateurs situés dans des référentiels différents ; une horloge en mouvement semble ralentie par rapport à une horloge immobile. Nous avons également rappelé que la relativité générale pose le principe d’équivalence entre l’accélération et la gravitation. En croisant ces deux principes, on peut en déduire que le temps s’écoule plus lentement dans un champ gravitationnel fort ! Ces effets, imperceptibles à notre échelle, sont cependant mesurables : deux horloges située au rez-de-chaussée et au 6e étage d’un immeuble se décalent inexorablement… Les satellites en orbite, qui subissent légèrement moins l’effet de la gravité, se trouvent de ce fait accélérés de 45 microsecondes par jour par rapport au temps mesuré à la surface de la Terre. Mais au voisinage d’un trou noir, où règne une gravité intense, ces effets sont considérablement amplifiés et deviendraient parfaitement perceptibles à nos sens ; quelques secondes passées à proximité de l’horizon des événements par un explorateur courageux semblera durer plusieurs années pour des observateurs restés tranquillement à l’abri dans leur vaisseau spatial situé à bonne distance du trou noir…
Bien, il est temps de passer à la pratique ! 🙂
Avec ces différents éléments, comment peut-on représenter de manière réaliste un trou noir ? Signalons qu’il existe en théorie 4 types de trous noirs différents – toujours de masse positive, mais avec ou sans rotation et avec ou sans charge électrique.
Pour simplifier, nous allons nous limiter à deux exemples :
- Un trou noir de Schwarzschild, sans rotation et sans disque d’accrétion ; hypothèse la plus simple et sans doute « trop » simple pour exister réellement.
- Un trou noir de Kerr, en rotation et doté d’un disque d’accrétion ; hypothèse qui semble la plus réaliste.
L’hypothèse « simple » du trou noir de Schwarzschild

Nous nous trouvons ici dans l’hypothèse la plus simple : un trou noir ponctuel, sans aucun mouvement de rotation et dépourvu de tout disque d’accrétion.
A défaut de matière environnante qui viendrait renforcer sa masse, on peut raisonnablement considérer pour l’exemple qu’il s’agit d’un trou noir peu massif, de quelques dizaines de masses solaires tout au plus, et donc très dense.
Dans ce cas de figure, le trou noir apparaîtrait sous une forme assez conforme à ce qu’on peut imaginer : un cercle parfaitement noir visible uniquement par contraste avec les astres situés en arrière-plan.
Pour autant, certains phénomènes interpellent immédiatement : si les objets éloignés du trou noir ne semblent pas affectés, ceux à proximité semblent déformés et dédoublés sous une forme inversée !
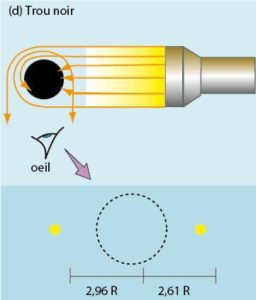
Il s’agit là d’une manifestation de l’un des effets évoqués précédemment, à savoir les mirages gravitationnels occasionnés par la forte courbure de l’espace-temps à proximité du trou noir, qui dévie les trajectoires des rayons lumineux.
Pour certains astres en arrière plan, leur lumière nous parvient après avoir suivi différentes trajectoires : l’une en directe (éventuellement déformée par le trou noir à l’image de la voie lactée en arrière-plan), et d’autres après avoir subi de fortes déviations.
On constate également que les images secondaires sont moins brillantes et plus rougies que les images primaires, conséquence de l’étirement de la longueur d’onde des photons dans le champ de gravitation.
En réalité, les rayons lumineux à proximité de l’horizon peuvent effectuer une infinité d’orbites autour du trou noir avant de s’échapper de son attraction : il existe donc une infinité d’images secondaires, de moins en moins lumineuses et de plus en plus rougies… En pratique, celles-ci sont de plus en plus proches du trou noir et il devient difficile de les distinguer de manière séparée…
Plus subtil mais plus spectaculaire : il est possible de voir les astres se trouvant derrière le trou noir !
Encore une fois, la forte déviation des rayons lumineux rend cet effet possible.
Pour les objets se trouvant « pile » derrière le trou noir du point de vue de l’observateur, la luminosité de ces derniers est même augmentée par effet de lentille gravitationnelle, mais leur image apparaît fortement déformée comme un arc parfaitement circulaire.
Encore plus impressionnant : il est même possible de voir la lumière émise par des astres situés… dans le dos de l’observateur !
Si vous regardez attentivement, vous pouvez en effet voir autour du cercle noir une sorte d’anneau de lumière qui l’entoure totalement.
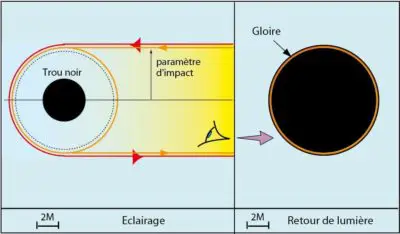
Cet anneau lumineux (appelé « gloire ») constitue en réalité un « retour de lumière » qui résulte de la trajectoire tellement déviée de la lumière que celle-ci repart dans la même direction que sa source d’origine. La lumière peut également réaliser plusieurs fois le tour du trou noir avant d’être renvoyée…
Mais cette « gloire » présente une autre caractéristique encore plus intéressante : son diamètre ne correspond pas à celui du trou noir. Les calculs démontrent que le diamètre visuel est en réalité 2,6 fois plus grand que le diamètre réel de l’horizon des événements.
Le trou noir apparaît donc visuellement 2,6 fois plus grand qu’il n’est en réalité !
L’hypothèse « réaliste » du trou noir de Kerr
Le trou noir « de Kerr » constitue le modèle de trou noir le plus vraisemblable : il n’y a en effet que peu de probabilité qu’un trou noir se trouve totalement dépourvu de rotation (ne serait-ce que lors de son effondrement initial…) et de matière environnante.
Ce modèle implique une différence importante avec le modèle de
Schwarzschild : la rotation du trou noir n’entraîne pas seulement une courbure de l’espace-temps à proximité, mais également une rotation de l’espace-temps lui-même.
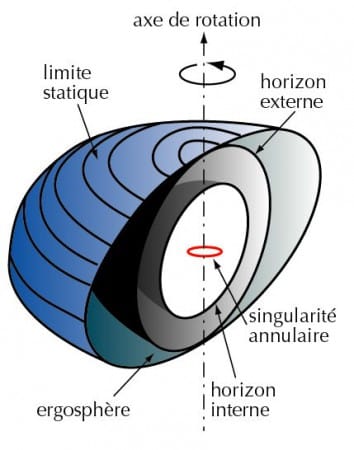
Cette rotation se traduit par un effet similaire à celui de l’aplatissement des pôles de la Terre ; avec un aplatissement de ce qui était ponctuel (ou sphérique) dans le cas du trou noir de Schwarzschild : la singularité et les orbites des rayons lumineux autour du trou noir. Dans le cas du trou noir de Kerr, ces orbites prennent la forme d’ellipses, plus ou moins allongées selon que les photons orbitent dans le sens de rotation du trou noir ou en sens inverse.
Décryptons le schéma ci-contre, afin de bien comprendre la structure des trous noirs de Kerr, plus complexe que celle des trous noirs ponctuels et fixes:
- Il existe bien sûr toujours une singularité centrale, mais celle-ci prend la forme d’un anneau. De manière surprenante, celle-ci n’est attractive que sur son plan équatorial… et devient répulsive dans les autres angles d’approches ! Il en résulte la création d’une « sphère de photons », subissant cette répulsion, autour de la singularité.
- Un horizon interne, sur lequel orbitent les photons tournant dans le même sens que le trou noir ;
- Un horizon externe, sur lequel orbitent les photons tournant dans le sens contraire du trou noir ;
- L’ergosphère, zone comprise entre la limite statique et l’horizon externe, au sein de laquelle aucune particule ne peut rester immobile et se retrouve entraînée dans le même sens de rotation que le trou noir. En réalité, un photon peut se retrouvé « immobile » s’il est émis dans le sens inverse de la rotation, car l’espace-temps lui-même est entraîné à la vitesse de la lumière par la rotation du trou noir !
- La « limite statique », en deçà de laquelle aucun objet ne peut rester immobile, même à la vitesse de la lumière. Ce phénomène, qui ne se produit qu’au niveau de l’horizon dans le cas des trous noirs statiques, n’implique toutefois pas que les particules qui s’y trouvent finissent obligatoirement par tomber dans le trou noir : elles peuvent au contraire y gagner de l’énergie et ressortir de cette zone, faisant perdre au trou noir une fraction de son moment angulaire…
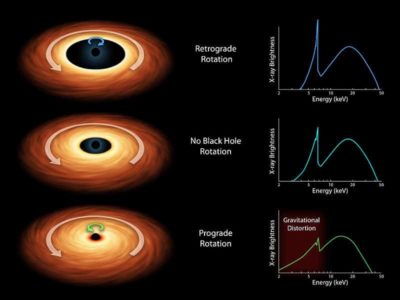
Dans le cas des trous noirs de Kerr possédant un disque d’accrétion, il est possible d’envisager que ce dernier soit en rotation dans le même sens que le trou noir (rotation prograde) ou en sens inverse (rotation rétrograde). Le sens de rotation du disque d’accrétion permet de mesurer, à partir de son spectre, le moment angulaire du trou noir. Par ailleurs, la rotation du disque d’accrétion par rapport à la rotation du trou noir influe sur le rayon de la « dernière orbite circulaire stable », en deçà de laquelle la lumière chute immanquablement dans le trou noir : cette dernière orbite stable est plus rapprochée du trou noir en cas de rotation du disque d’accrétion dans le même sens que le trou noir. Le rayon de la dernière orbite circulaire stable est située à 3 fois le rayon de Schwarzschild pour un trou noir sans rotation, mais peut diminuer jusqu’à 0,6 fois ledit rayon pour un trou noir de Kerr présentant une rotation maximale.
Comment représenter cette fois un tel trou noir ?

Très simplement, celui-ci a la forme d’une sphère, entourée d’un disque d’accrétion plat, situé dans le plan de rotation ; de manière similaire à une planète entourée d’anneaux, telle que Saturne… Voici pourtant ci-contre la première représentation réaliste d’un tel trou noir, réalisée par Jean-Pierre Luminet en 1979… assez éloignée de l’image de Saturne ! Comment expliquer la différence entre la réalité physique de l’objet et son aspect ?
Là encore, l’explication tient à la déformation extrême de l’espace-temps au voisinage du trou noir, qui dévie très fortement les rayons lumineux émis par le disque d’accrétion.

L’image ci-contre permet de mieux comprendre les déformations à l’oeuvre autour du trou noir, qui affectent la perception visuelle de l’ensemble.
En haut à gauche, est représenté le trou noir (une sphère invisible…) entouré d’un disque d’accrétion décomposé en plusieurs orbites différentes selon les vitesses des particules. Dans cette représentation « théorique » et idéale, on voit que le disque est en réalité parfaitement plat, à l’image des anneaux de Saturne.
Si l’on tient compte de la déformation de l’espace-temps, la représentation visuelle change radicalement, puisqu’il est possible de voir l’ensemble du disque d’accrétion, y compris la partie se trouvant derrière le trou noir ! Cela était possible déjà dans le cas du trou noir statique, mais ici la présence du disque d’accrétion rend cet effet encore plus impressionnant.
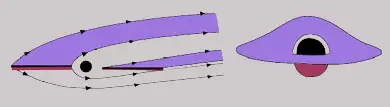
Plus incroyable encore, il est même possible de voir cette partie arrière à la fois sous sa face supérieure et sous sa face inférieure ! Les rayons lumineux émis sur la face supérieure sont déviés vers l’observateur « par dessus » le trou noir (formant ainsi l’a déformation supérieure) ; tandis que les rayons lumineux émis par la face inférieure sont quant à eux déviés sous le trou noir avant de revenir vers l’observateur (formant l’arc de cercle inférieure).

Si l’on tient compte, enfin, du fait que le disque d’accrétion est en rotation, il faut également représenter le fait que l’un des côtés du disque est plus lumineux et « bleui » (celui s’approchant de l’observateur) et que l’autre côté est moins lumineux et « rougi » (celui s’éloignant de l’observateur).
Avec l’ensemble de ces paramètres, il est possible de représenter un trou noir de Kerr de manière réaliste, comme dans l’exemple ci-contre, réalisé par Kip Thorne dans le cadre de la modélisation du trou noir « Gargantua » du film Interstellar.
Pour les cinéphiles avertis, il ne vous aura pas échappé que cette représentation est assez différente de celle finalement retenue dans le film, où le disque est parfaitement circulaire et sans atténuation de luminosité ou de variations de couleurs… En effet, si Kip Thorne et son équipe avait simulé l’aspect du trou noir de manière réaliste, le réalisateur Christopher Nolan a décidé de s’en tenir à une représentation plus « simple », au motif que le public « n’aurait pas compris »… Mais vous ne faites désormais plus partie de cette catégorie du « public » ! 🙂
Attention cependant, si la théorie de la relativité générale fournit des outils capables de nous aider à représenter l’aspect d’un trou noir vu de l’extérieur, il ne faut pas perdre de vue que celle-ci peine à décrire l’intérieur d’un trou noir, et en particulier la zone de « singularité » centrale, qui défie pour l’instant toute modélisation. Dans cette zone, où la densité tend vers l’infini, les équation de la relativité générale ne donnent plus de résultat pertinent et surtout ne sont plus adaptées pour décrire le comportement de la matière à cette échelle où la mécanique quantique règne en maître. Pour aller plus loin dans notre compréhension de l’intérieur des trous noirs, il faudrait donc développer une théorie quantique de la relativité, qui permette de concilier les postulats de ces deux théories… un tour de force qui demeure à ce jour l’un des plus grands défis de la physique !
Maintenant que nous sommes armés de toutes ces informations théoriques… confrontons-les à la réalité, avec les différents modes de détection des trous noirs et en particulier la première « vraie » image obtenue par l’EHT !
3. Mettre en lumière les trous noirs !
L’astronomie est une science qui présente une particularité notable par rapport aux autres disciplines : il est impossible d’accéder réellement aux objets étudiés (en tout cas en dehors du système solaire…). L’étude des astres ne peut se faire que par l’observation, et notamment par l’analyse de la lumière émise par ces derniers.
Dans le cas des trous noirs, cela est un peu plus problématique puisque ces astres n’émettent – par définition – aucun rayonnement !
Ce seul point est déjà en lui-même suffisamment gênant pour envisager de les détecter, mais il y a encore d’autres contraintes qui compliquent encore plus cette tâche. Tout d’abord, comme nous l’avons vu, les trous noirs sont des objets extrêmement compacts : seulement quelques dizaines de kilomètres de diamètre pour des trous noirs stellaires… Inutile de dire que la détection d’un astre aussi petit, même situé à une distance assez proche du système solaire (quelques dizaines d’années-lumière par exemple) constitue un vrai défi. Il est bien sûr possible d’essayer de détecter les déviations des rayons lumineux – les mirages gravitationnels – occasionnés par le trou noir, mais ceux-ci ne sont clairement visibles qu’aux abords immédiats de celui-ci… et donc difficilement détectables à grande distance. De très nombreux trous noirs de ce type ont cependant déjà été détectés, grâce à la présence d’une étoile compagnon, dont le plus proche se situe à environ 1600 années-lumière de la Terre.
Pour les trous noirs supermassifs, leurs dimensions offrent un peu plus d’espoir. Le fait qu’ils soient entourés de matière offre une chance supplémentaire. Mais ceux-ci ne sont situés que dans les noyaux des galaxies… Malheureusement le centre de notre propre Galaxie est difficile à observer directement en raison de la grande quantité de matière dans cette direction… et notre plus proche voisine se trouve à plus de 2 millions d’années-lumière !
L’observation de certains phénomènes très énergétiques constitue une forte suspicion de la présence de trous noirs : c’est le cas par exemple du jet de plasma observé dans le noyau de la galaxie M87, ou encore de la forte source de rayons X Cygnus X-1 que nous avons déjà évoquée. Mais il ne s’agit dans ces cas que d’une « forte présomption » et non d’une détection certaine. Il existe par exemple des théories alternatives reposant sur des étoiles à neutrons, ou des couples binaires de tels astres massifs, permettant d’expliquer plus ou moins les phénomènes observés sans qu’il soit nécessaire de recourir aux trous noirs…
Nous allons voir cependant que l’existence des trous noirs a déjà pu être démontrée par certaines observations « indirectes » ; avant la consécration que constitue l’observation directe du trou noir M87*.
Les méthodes de détection « indirectes »
Sagittarius A* : des étoiles qui orbitent autour de… rien !
Si un trou noir n’émet aucun rayonnement, sa masse l’empêche cependant de passer totalement inaperçu…
En effet, cette masse produit une déformation de l’espace-temps très importante, qui va altérer les trajectoires des objets passant à proximité. Si l’on observe des astres dotés de trajectoires ou d’orbites étranges, il y a fort à parier qu’un objet massif soit à l’origine de ces mouvements… et si l’objet en question ne peut pas être décelé par des moyens optiques, seul un trou noir peut expliquer de telles anomalies.
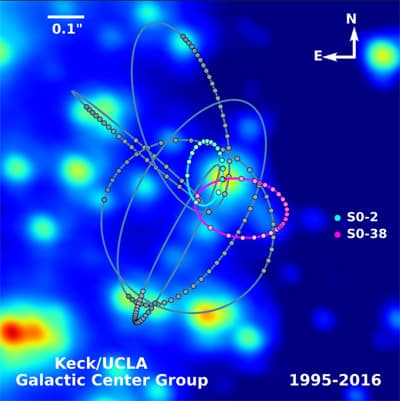
C’est ainsi qu’au centre de notre galaxie, les astronomes ont observé pendant une quinzaine d’années le mouvement des étoiles situées à proximité de l’endroit où l’on suspecte l’existence du trou noir supermassif Sagittarius A*. Comme le montre l’animation ci-contre, le résultat est très surprenant : les étoiles orbitent autour d’un objet… invisible !
En connaissant la vitesse des étoiles et l’axe de leur orbite, il est possible de déterminer la masse du corps central : plus de 4 millions de masses solaires. Pourtant, malgré cette masse colossale, aucun objet n’est visible.
Il n’y a donc guère de doute quant au fait que ces étoiles (elles bien visibles alors qu’elles ne représentent au mieux que quelques masses solaires), sont en orbite autour du trou noir supermassif au centre de notre galaxie, nommé Sagittarius A*.
Dans la mesure où il n’existe dans la théorie actuelle aucun astre disposant d’une telle masse et n’émettant aucun rayonnement en dehors des trous noirs, on peut considérer qu’une telle observation constitue une preuve « indirecte » de leur existence.
La détection des ondes gravitationnelles générées par la coalescence de 2 trous noirs
Quand on évoque « l’espace-temps », on pourrait se figurer qu’on désigne sous ce terme une notion abstraite, certes commode à notre esprit pour pouvoir se représenter ce dont on parle, mais sans réalité physique derrière… Pourtant, cette représentation simplifiée d’un « tissu » d’espace est également, en grande partie, assez réaliste !
Dès lors qu’il ne s’agit pas seulement d’un cadre formaliste pour décrire les phénomènes physiques qui s’y déroulent, mais bien d’une réalité tangible, peut-on envisager qu’il existe d’autres modifications de l’espace-temps que sa courbure qui puissent être décelés ?
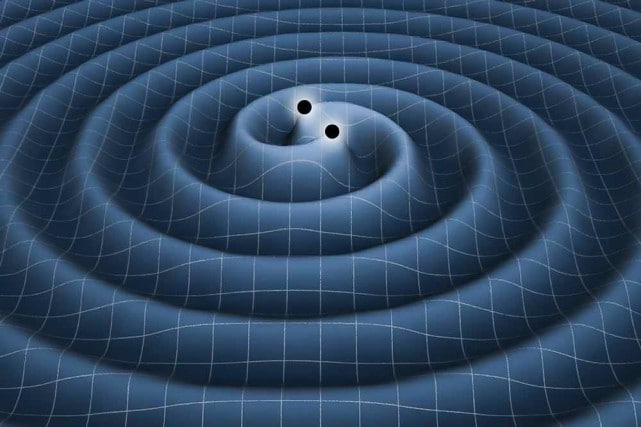
Crédits : K. Thorne (Caltech), T. Carnahan (NASA GSFC)
Dès 1916, Albert Einstein lui-même tire une conclusion directe de ses équations en effectuant l’une des plus célèbres – et spectaculaires – prédictions de l’histoire de la physique : la gravitation peut se matérialiser sous la forme « d’ondes » se propageant dans l’espace-temps à la vitesse de la lumière.
De telles « ondes gravitationnelles » sont ainsi créées par des masses importantes en mouvement… mais même avec des astres de masses considérables ou dans le cadre d’éventements très énergétiques, les ondes gravitationnelles qui sont émises demeurent imperceptibles à notre échelle. Cette prédiction demeure donc purement théorique jusqu’en 1974, où une preuve indirecte de l’existence de telles ondes est obtenue par l’étude de l’orbite d’un pulsar binaire. A chaque orbite, la période de révolution des pulsars diminue de manière certes très faible, mais mesurable : cette diminution de la période orbitale correspond parfaitement aux prédictions de la relativité générale, et est occasionnée par la dissipation d’une fraction de l’énergie du système sous la forme d’ondes gravitationnelles. Cette découverte fût considérée comme suffisamment crédible quant à l’origine du phénomène pour que les astronomes à l’origine de cette étude se voient décerné le Prix Nobel de physique en 1993.
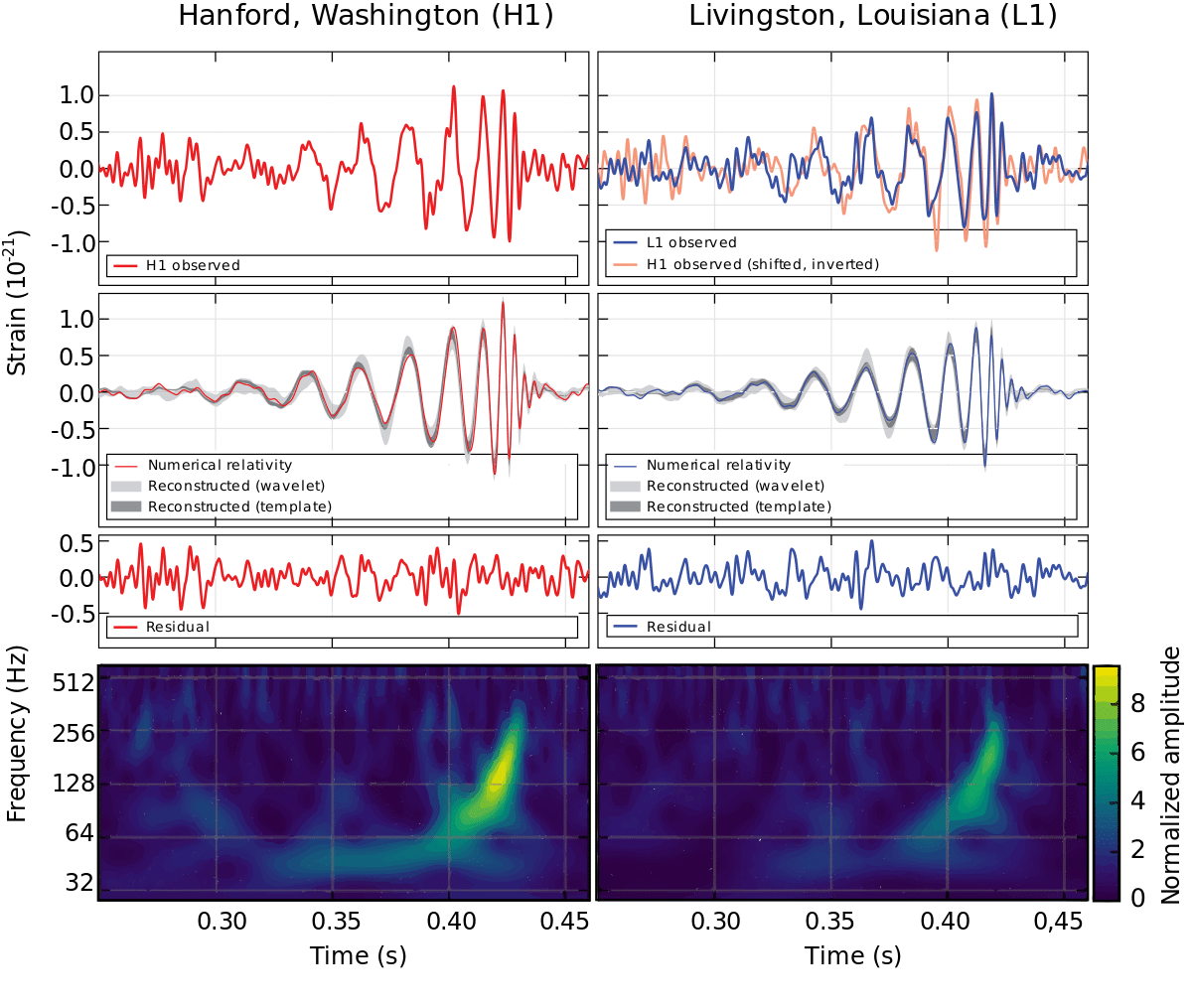
La réalité des ondes gravitationnelles était dès lors fermement établie, mais il a fallu attendre le 11 février 2016 pour que les chercheurs du LIGO (Laser Interferometer Gravitational-Wave Observatory) annoncent avoir observé directement et pour la première fois une onde gravitationnelle.
Bien que ce signal ait été capté en septembre 2015, son origine remonte à plus de 1,3 milliards d’années, lors de la fusion (coalescence) de deux trous noirs de 36 et 29 masses solaires !
Ces deux trous noirs, tournant autour de leur centre de gravité, ont orbité en spirale de plus en plus rapprochée, pour finalement fusionner en un seul trou noir « de Kerr » de 62 masses solaires. La différence, soit une masse équivalente à 3 Soleils, a été dissipée quasiment instantanément sous la forme d’ondes gravitationnelles ; les deux trous noirs tournoyant dans les dernières fractions de seconde à 60% de la vitesse de la lumière !
Nous n’allons pas rentrer dans le détail du fonctionnement de LIGO, ni des ondes gravitationnelles, mais précisons qu’une telle mesure équivaut à mesurer des fluctuations de l’espace-temps de l’ordre du milliardième de la taille d’un atome ! Malgré les forces en jeu (50 fois plus d’énergie dégagée en 0,2 secondes que l’ensemble de la puissance rayonnée par toutes les étoiles de l’Univers…) , les effets sont donc incroyablement faibles à notre échelle ; et leur mesure constitue un véritable tour de force technologique.
Les mesures obtenues sont tellement proches à celles prévues par la théorie de la relativité générale que cette fois plus aucun doute n’est permis : les équipes de LIGO ont bel et bien observé « en direct » les fluctuations de l’espace-temps issu du passage d’ondes gravitationnelles émises il y a plus d’un milliard d’années par la fusion de 2 trous noirs. Précisons également qu’en l’état de nos connaissances, aucun objet autre qu’un trou noir n’est susceptible de générer les ondes captées par LIGO.
Ces mesures sont tellement précises et si bien en accord avec la théorie que certains chercheurs considèrent que cette détection est en réalité la première « preuve directe » – et non indirecte – de l’existence des trous noirs.
Depuis cette première observation historique, 3 autres détections ont été réalisées ; dont la dernière avec l’ensemble des instruments existants, dont l’instrument européen VIRGO, ce qui a permis de déterminer la direction du signal. Une amélioration des instruments devrait permettre à terme, selon les physiciens, de détecter une fusion de trous noirs toutes les heures !
Les enseignements de ces premières découvertes sont donc extraordinairement riches : première détection directe des ondes gravitationnelles, première réelle confirmation de l’existence des trous noirs, confirmation que ces derniers peuvent fusionner, mais également que de tels phénomènes sont très fréquents… et donc qu’il doit exister un très grand nombre de trous noirs dans l’Univers. Et plus encore, cette détection ouvre la voie à une « nouvelle astronomie », avec la possibilité d’observer l’Univers au-delà de la lumière – visible ou invisible, au moyen des ondes gravitationnelles…
Malgré tout, le défi ultime consistait encore à pouvoir observer directement et de manière « classique » (par le biais des ondes électromagnétiques, c’est à dire la lumière) un trou noir… défi qui vient donc d’être relevé par les chercheurs de la collaboration EHT.
M87* : voir l’invisible !
Comme nous l’avons déjà évoqué, les trous noirs peuvent être très compacts et très denses, ou bien être « supermassifs » et très peu denses. Dans le premier cas, ces trous noirs sont le résultat de l’effondrement d’une étoile sur elle-même ; et l’on estime qu’il peut en exister plusieurs millions au sein d’une même galaxie. Les nombreuses détections par les instruments LIGO et VIRGO, pourtant dans leur phase initiale de fonctionnement, laissent à penser que ce nombre pourrait être bien plus élevé encore… Dans le second cas, les trous noirs « supermassifs » se trouvent au centre des galaxies. Il est aujourd’hui admis que l’ensemble des galaxies de grande taille contiennent en leur centre au moins un trou noir supermassif, de l’ordre d’une dizaine de millions à plusieurs milliards de masses solaires. Certaines galaxies renfermeraient même des trous noirs supermassifs binaires, en rotation l’un autour de l’autre…
La question de l’origine de ces trous noirs supermassifs reste cependant encore largement débattue. L’idée d’une accrétion de matière continue sur plusieurs milliards d’années n’est pas pleinement satisfaisante, car l’existence de tels trous noirs a été démontrée dans des galaxies à fort décalage spectral, c’est à dire dans des galaxies observées à un âge très précoce de l’Univers. Il est donc vraisemblable que l’origine de tels trous noirs soit à rechercher dans les premiers temps de l’Univers, par exemple par l’effondrement sur eux-mêmes d’immenses nuages de gaz aujourd’hui introuvables dans l’Univers observable… La question n’est même pas encore tranchée de savoir si les trous noirs se forment au sein des galaxies une fois celles-ci constituées, ou au contraire si les galaxies se forment autour de trous noirs supermassifs préexistants.
Pour réaliser une photographie d’un trou noir, il est donc préférable d’envisager un trou noir supermassif qui présente plus d’avantages qu’un trou noir stellaire. Le premier – et non des moindres – est qu’il est relativement simple d’estimer sa localisation, à savoir au centre d’une galaxie ! Le second avantage est qu’un tel trou noir dispose d’une masse considérable, qui permet d’espérer mesurer ses effets de manière plus évidente à longue distance. Enfin, un trou noir supermassif se situant dans une zone où la densité de matière est très importante, ceux-ci doivent disposer d’un disque d’accrétion permettant de les révéler plus simplement… voire d’être à l’origine de phénomènes très énergétiques et décelables de manière classique, comme une source de rayons X ou gamma, ou encore de jets de matière, comme dans le cas de la galaxie M87 ; cible retenue par la collaboration EHT pour la première image d’un trou noir.

Cette galaxie géante présente un noyau actif, dont l’activité se manifeste par l’émission d’un puissant rayon de plasma qui s’étend sur plus de 5000 années-lumière. Autant d’indices de la présence d’un trou noir supermassif en son centre … et donc un candidat idéal pour tenter de réaliser la première image d’un trou noir !
L’image réalisée par l’Event Horizon Telescope nous propose ainsi une plongée au cœur de la galaxie M87, située à 55 millions d’années-lumière, au sein de laquelle se trouve l’un des trous noirs les plus massifs connus, « M87* », d’une masse estimée de 6,5 milliards de masses solaires.
Il faut dire que la galaxie M87 est, en elle-même, un véritable « monstre » : il s’agit de l’une des galaxies les plus massives connues. Si ses dimensions « visibles » dépassent légèrement celles de notre Voie Lactée, son halo s’étend en revanche sur 1 million d’années-lumière, soit environ 3 fois le diamètre du halo de notre galaxie. Sa masse est par ailleurs bien supérieure avec plus de 4000 milliards de masses solaires : s’il est difficile d’estimer avec précision les masses des galaxies – y compris de la nôtre – certains chercheurs estiment que la masse totale de M87 pourrait représenter jusqu’à 200 fois la masse de la Voie Lactée !
Pour le plaisir, effectuons donc cette plongée au cœur de la galaxie M87, afin de découvrir le trou noir supermassif M87* :
L’image obtenue peut sembler a priori assez éloignée de ce que nous avons évoqué précédemment, et notamment des simulations réalistes qui ont pu être présentées… Quelques explications s’imposent pour bien comprendre ce que montre cette image.
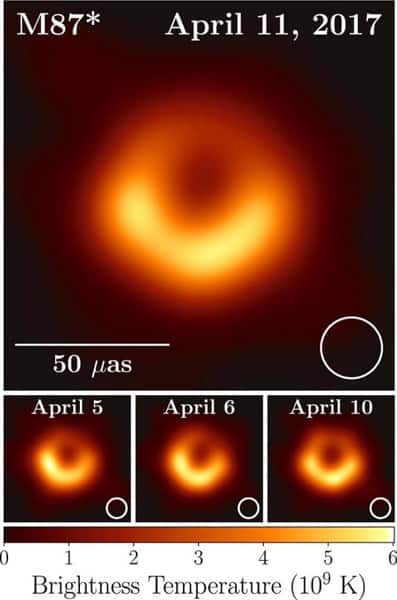
La première chose à souligner, c’est que le résultat en question n’est pas une « photographie » au sens propre, mais une image reconstituée d’après de multiples données issues de différents radiotélescopes (comme nous l’expliquerons dans la section suivante) et surtout celle-ci est en couleurs « codées » : les observations ont été réalisées uniquement dans le domaine radio millimétrique (1,3mm de longeur d’onde) et ne contiennent donc aucune information relative aux « couleurs » (ce qui n’aurait de toute manière guère de sens dans le domaine radio, hors du spectre visible…).
La gamme de couleurs utilisée représente en réalité la « température de brillance », c’est à dire la température d’un corps noir qui émettrait la même intensité de rayonnement à la longueur d’onde considérée que celle mesurée pour l’objet cible. L’image aurait donc pu être présentée en dégradé de gris, de bleu ou de vert, le résultat n’aurait pas été différent ni moins réaliste !
Il faut donc insister sur le fait que, même si l’image peut sembler « floue » de prime abord, il ne s’agit pas d’une photographie mais davantage d’une « interprétation visuelle » de données radio, pour laquelle la notion de « netteté » n’est pas tout à fait comparable !
S’agissant d’une image créée d’après des données radio recombinées, l’aspect final dépend grandement des choix de traitements et d’algorithmes utilisés. La collaboration EHT a ainsi publié différentes versions d’images obtenues par 4 équipes différentes qui ont traité exactement les mêmes données de départ, de manière totalement indépendante. Comme on peut le voir dans les images ci-dessous, les résultats visuels sont loin d’être identiques !
Cependant, ils sont tous suffisamment globalement cohérents pour que l’aspect visuel général présenté sous la version finale puisse être considéré comme crédible.
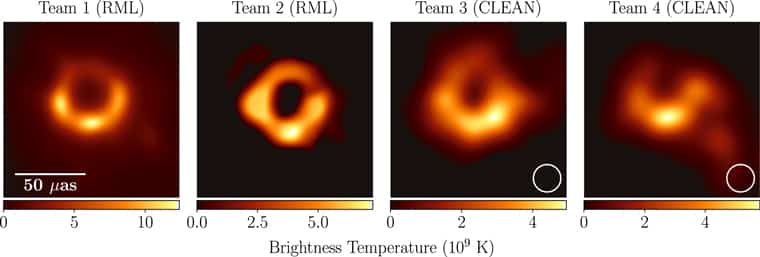
Différentes images de M87* obtenues à partir des mêmes données. Crédits : EHT collaboration.
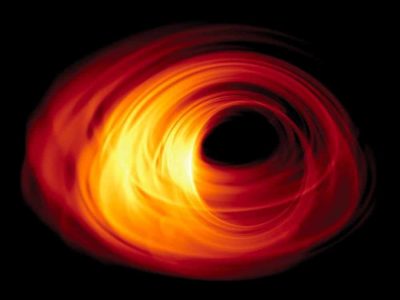
Sur cette image, M87* est vue selon un angle de 60° : beaucoup plus que la plupart des simulations réalisées sur lesquelles, pour mieux visualiser le phénomène de distorsion des rayons lumineux, un angle plus petit est souvent retenu (la première simulation réalisée par Jean-Pierre Luminet était basée sur un angle de 15°, tandis que celle de Kip Thorne était quasiment dans le plan du disque d’accrétion).
Dans le cas de M87*, le trou noir est davantage vu « de dessus » que par la tranche… Il est donc parfaitement logique que l’aspect général de l’image de M87* ne corresponde pas exactement aux simulations présentées dans la section précédente ; la différence d’angle de vue ayant de grandes répercussions dans les effets de mirage gravitationnels.
La simulation ci-contre (réalisée hors du cadre de la collaboration EHT), montre l’apparence d’un trou noir de Kerr avec un disque d’accrétion, visualisé sous un angle plus proche de celui de M87* : la ressemblance est déjà plus frappante.
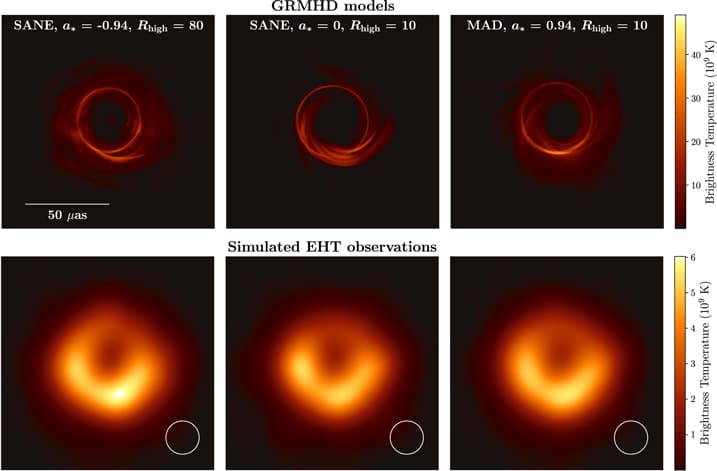
Ci-contre, d’autres simulations, réalisées cette fois dans le cadre de l’EHT, qui mettent en relation différentes représentations « réalistes » de ce qu’il serait possible de visualiser avec une meilleure résolution (en haut) et les aspects visuels estimés des observations par l’EHT (en bas), intégrant les différentes limitations de résolution : la correspondance avec les images réellement obtenues est quasi-parfaite !
On voit également bien la forte asymétrie du disque d’accrétion, avec un côté plus brillant et un côté plus sombre, conforme aux prévisions de la relativité générale, à l’effet doppler et en accord avec les simulations évoquées précédemment.
Les observations successives, réalisées sur plusieurs nuits consécutives, montrent également que le trou noir est en rotation (dans le sens des aiguilles d’une montre sur l’image).

Même si ce point a déjà été évoqué précédemment, rappelons que le trou noir lui-même n’est pas réellement visible sur cette image, mais n’est visible qu’en « ombre chinoise », par contraste avec la luminosité de la matière échauffée en rotation dans le disque d’accrétion environnant.
Pour la même raison que celle expliquée ci-dessus dans le cas du trou noir de Schwarzschild, le diamètre apparent du trou noir est 2,6 fois plus grand que son diamètre réel, matérialisé par l’horizon des événements (représenté sur l’image ci-contre par le cercle noir). Cet horizon a un diamètre de 38 milliards de kilomètres, soit environ 3 fois l’orbite de Pluton autour du Soleil. Comme nous l’avons déjà évoqué, c’est la mesure de ce diamètre qui permet de déterminer la masse du trou noir.
Au final, du fait de la parfaite correspondance avec les simulations, cette image constitue donc une remarquable confirmation de la théorie de la relativité générale, ici testée jusque dans ses plus extrêmes limites au plus proche de l’horizon d’un trou noir supermassif !

Elle permet aussi de lever le voile sur une partie du mystère liée à l’origine du jet de plasma observé sur la galaxie M87.
Grâce au télescope Chandra, qui observe l’Univers en rayon X, il est possible de situer le trou noir au sein d’une image plus large (ci-contre). On constate que le jet est dirigé dans une direction perpendiculaire au disque d’accrétion du trou noir, aligné avec l’axe de rotation de M87*.
Cela confirme, comme le pensaient déjà les astrophysiciens, qu’un tel jet trouve son origine dans les très forts champs gravitationnels et magnétiques générés à la fois par le trou noir et son disque d’accrétion en rotation rapide (jusqu’à 1000 km/s).
L’image montre également de nombreuses boucles de gaz émettant fortement en rayons X ; ces concentrations étant créées par des ondes de choc générées par les variations d’éjection de matière dans le jet. Ces variations, légères ou brutales, semblent se répéter à des intervalles assez réguliers dont le mécanisme est encore mal compris. Il apparaît également que le trou noir est décalé d’environ 80 années-lumière du centre de la galaxie, phénomène qui n’est encore pas clairement expliqué…
Malgré ces exceptionnels résultats de recherche, de nombreuses zones d’ombres demeurent donc encore à expliquer !
Mais, au-delà de cette image historique en elle-même, il convient de dire quelques mots à propos de la technique mise en oeuvre pour parvenir à ce résultat, qui est tout autant spectaculaire…
4. Comment cette image a-t-elle été réalisée ?
Sur les images de M87* ci-dessus, vous avez sans doute remarqué l’échelle indiquée : « 50 µas« , c’est à dire 50 microsecondes d’arc.
Une rapide explication s’impose ici, pour ceux qui ne seraient pas familiarisés avec l’unité d’angle en question. Un cercle se compose de 360 degrés ; chaque degré se compose de 60 minutes d’arc ; et chaque minute d’arc se compose de 60 secondes d’arc. Un degré contient donc 3600 secondes d’arc… hors, ici, l’échelle se compte en millionièmes de seconde d’arc ! Vous l’avez compris, l’angle envisagé ici est infime : 50 µas équivaut à 1/ 72 000 000e de degré !
Pour comparaison, la Lune a un diamètre apparent de 0,5° (soit 30 minutes d’arc), Jupiter 45 secondes d’arc, et Pluton 0,1 seconde d’arc… Pourtant, sur cette dernière planète, même le télescope spatial Hubble ne parvient que difficilement à déceler quelques détails…
L’animation ci-contre montre ce que représente la taille apparente de M87* par rapport à un seul pixel de la caméra WFC3 du télescope spatial, qui dispose d’une focale de 57,6 mètres et dont la résolution n’est limitée que par les lois de l’optique !
M87* ne représente qu’une infime fraction d’un seul pixel de la caméra… inutile de préciser qu’il est impossible d’envisager la moindre image de ce trou noir par des moyens optiques traditionnels…
L’explication de cette taille apparente infime est simple : M87* est certes l’un des plus gros trous noirs connus, de 6,5 milliards de masses solaires et de 38 milliard de kilomètres de diamètre pour son horizon… mais il est situé à 55 millions d’années-lumière (1 année-lumière représentant 10 000 milliards de kilomètres)…
Plusieurs images très parlantes ont été utilisées pour essayer de visualiser une telle dimension apparente : l’équivalent de lire un journal posé à Paris depuis New-York, ou encore voir une balle de golf posée sur la Lune… Personnellement, j’aime aussi l’idée que cela correspond à la taille d’un atome tenu à bout de bras !
Le pouvoir de résolution d’un instrument d’optique dépend de 2 facteurs : la diamètre de l’instrument, et la longueur d’onde observée, selon la formule ci-contre (l’angle est exprimé en radians). Si nous nous amusons à calculer le diamètre de l’instrument nécessaire pour obtenir la résolution atteinte pour réaliser l’image de M87* à la longueur d’onde de 1,3mm, nous trouvons que celui-ci doit avoir… le diamètre de la Terre !
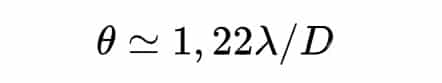
Naturellement, il est inenvisageable de construire un instrument de cette dimension… mais il existe une technique permettant de créer virtuellement un observatoire aussi démesuré : l’interférométrie.
Sans rentrer dans les détails (très complexes) de cette technique, disons simplement que l’interférométrie consiste à combiner les signaux reçus par différents télescopes ou instruments, afin de créer un télescope « virtuel » d’un diamètre correspondant à la distance entre les deux instruments ; et disposant donc d’un pouvoir de résolution accru d’autant !
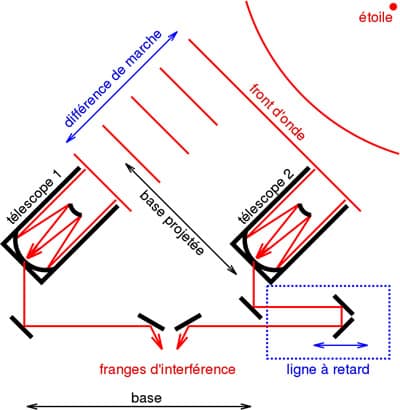
Seule (petite…) difficulté : pour recombiner les signaux reçus par les différents instruments, il faut que ceux-ci soient « en phase », c’est à dire qu’il soit possible de reconstituer un « front d’onde » cohérent. Autrement dit, les signaux recombinés doivent avoir eu le même temps de parcours depuis la source lumineuse… ce qui pose un problème évident puisque les différents signaux sont reçus par des différents situés à des endroits différents, et donc à des moments qui ne sont pas strictement identiques ! Difficulté supplémentaire : la combinaison des signaux doit être réalisée avec une précision inférieure à la longueur d’onde d’observation.
L’interférométrie est donc plus simple à mettre en oeuvre pour des observations à de grandes longueurs d’onde, par exemple dans le domaine radio. Dans le domaine optique ou proche infra-rouge, comme cela est réalisé au Very Large Telescope (VLT) européen, les 4 télescopes peuvent être utilisés en mode interférométrique, et la recombinaison des signaux s’effectue en temps réel, à l’aide de « lignes à retard » qui permettent de synchroniser temporairement les différents signaux, reçus à quelques dizaines de mètres d’écart.
En interférométrie radio, où les instruments sont bien plus éloignés, il est impossible d’utiliser une telle technique. Les signaux reçus par chacun des instruments sont donc enregistrés sur support physique et datés avec la plus grande précision à l’aide d’une horloge atomique. La recombinaison s’effectue a posteriori, à l’aide de supercalculateurs et d’algorithmes spécifiques.
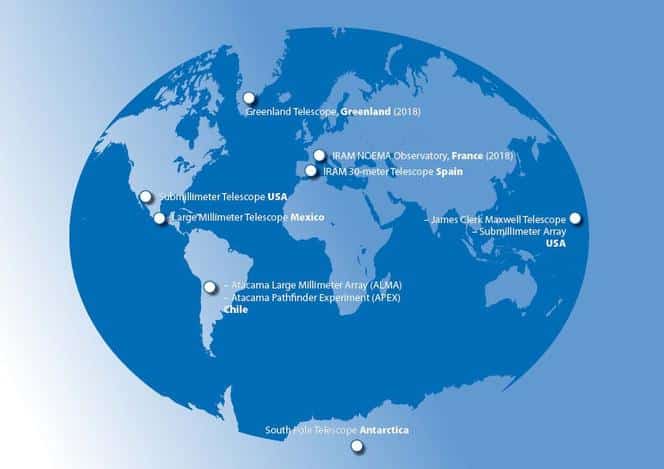
Pour réaliser l’image de M87*, la collaboration EHT a effectivement retenu l’observation dans les ondes radio millimétriques, qui sont fortement émises par le trou noir et son disque d’accrétion et qui ont l’avantage de traverser assez facilement le milieu interstellaire. L’EHT a , à cette fin, utilisé 8 instruments radio très performants, répartis dans différentes régions du globe, afin de reconstituer un instrument « virtuel » d’un diamètre de 10 000 kilomètres !
Autre difficulté, l’ensemble des instruments doit observer l’astre cible au même moment : compte-tenu de la localisation différente des instruments, les dates où une telle observation est possible sont donc réduites… et encore faut-il que la météo soit favorable sur tous les sites, avec un ciel dégagé et faible en vapeur d’eau (qui absorbe les ondes millimétriques). Un tel créneau d’observation a été possible pendant une semaine au mois d’avril 2017, au cours de laquelle les acquisitions ont été réalisées.

Mais une fois les observations réalisées, les choses sérieuses ne font que commencer ! Alors qu’on pourrait penser qu’il n’y a là aucune difficulté particulière, l’envergure démesurée du projet transforme même la réunion de toutes les données en un premier défi. En effet, le volume de données enregistrées ne se compte plus en gigaoctets, ni en téraoctets, mais en pétaoctets : 4 Po de données, soit 4000 To (ou encore 4 000 000 Go) ! Avec un tel volume, impossible de transférer les données par internet : le transfert physique des disques durs, par avion, est plus rapide… Et il a fallu attendre 6 mois pour récupérer par hélicoptère les données à l’observatoire du Pôle Sud.
Une fois les données récupérées, elles ont été confiées à deux équipes distinctes, au MIT et à l’Institut Max Planck, afin d’être traitées de manière indépendante pour pouvoir croiser les résultats finaux, qui se sont révélés cohérents.
La phase de traitement des données aura ainsi duré de nombreux mois, pour que l’image finale soit présentée, 2 ans après la collecte des données…
Seule ombre au tableau, les données sur Sagittarius A*, le trou noir supermassif au centre de notre Voie Lactée, ne se sont pas avérés exploitables… il faudra donc encore attendre quelques années pour espérer voir celui-ci.
Conclusion : qu’attendre de plus dans les années à venir ?
La réalisation de cette première image d’un trou noir est sans conteste l’un des plus grands exploits de la physique moderne, d’une importance égale à la détection des ondes gravitationnelles ou du boson de Higgs.
Mais l’exploit à peine digéré, on se prend à rêver de récidives encore plus impressionnantes dans les prochaines années, à l’aide de cette technique d’observation étendue à l’échelle planétaire…
La collaboration EHT s’est en effet enrichie de nouveaux instruments, dont un situé au Pôle Nord, ce qui va permettre d’accroître la base de l’instrument virtuel, et donc sa résolution. L’observation à une longueur d’onde inférieure (0,8mm au lieu de 1,3mm) permettra également un gain en résolution significatif (35%). Une prochaine étude est également en cours, qui devrait révéler la polarisation du trou noir, et donc révéler si les trous noirs disposent d’un champ électromagnétique intrinsèque…
La collaboration EHT devrait ainsi disposer des outils et du savoir-faire permettant de révéler plusieurs dizaines, voire centaines de trous noirs dans des galaxies proches… et bien sûr, celui situé au centre de notre propre Voie Lactée, Sagittarius A*.
Et, après tout, pourquoi se « limiter » à un instrument du diamètre de la Terre, puisqu’il est possible d’envoyer dans l’espace des instruments situés à des positions éloignées de plusieurs centaines de milliers de kilomètres, et ainsi disposer d’un pouvoir de résolution encore plus incroyable ?
Pour aller plus loin…
Quelques recommandations de lecture et de ressources si vous souhaitez approfondir certains sujets abordés dans cet article :

Les trous noirs – A la poursuite de l’invisible
Astrophysique
Alain Riazuelo – De Boeck (2018) – 194 pages
Difficulté : 
 (2 / 5 ouvrage s'adressant aux débutants, ou de vulgarisation scientifique simplifiée.)
(2 / 5 ouvrage s'adressant aux débutants, ou de vulgarisation scientifique simplifiée.)
Un ouvrage d’initiation pour comprendre les mystères des trous noirs, par l’un des meilleurs spécialistes mondiaux.
Alain Riazuelo parvient à rendre accessibles les motions les plus complexes, en évitant l’écueil (dans lequel tombe bon nombre de livres de vulgarisation sur le sujet…) d’une simplification si importante que l’ouvrage s’en trouve dépourvu d’intérêt.
L’ouvrage est complété par une simulation vidéo très intéressante ; dont un petit aperçu est visible dans cet article.

Le destin de l’Univers
Astrophysique – Cosmologie
Jean-Pierre Luminet – Fayard (2006) – 592 pages
Difficulté : 
 (3 / 5 ouvrage s'adressant à un public amateur, possédant déjà quelques notions dans la matière abordée, ou de vulgarisation scientifique sérieuse mais sans recours à des équations.)
(3 / 5 ouvrage s'adressant à un public amateur, possédant déjà quelques notions dans la matière abordée, ou de vulgarisation scientifique sérieuse mais sans recours à des équations.)
Avec une passion communicative, Jean-Pierre Luminet nous entraîne dans le labyrinthe du « destin » de l’Univers, peuplé de créatures mystérieuses (énergie noire…) ou inquiétantes (hypernovæ, trous noirs…), mais toujours fascinantes.
Une plongée abyssale dans le maelstrom cosmique, où la gravitation règne en maître absolu.
Plus qu’un ouvrage de vulgarisation remarquable : une balade mentale hypnotique et d’une intelligence rare. Indispensable !

Les trous noirs
Astrophysique – Cosmologie
Jean-Pierre Luminet – Seuil (1992) – 395 pages
Difficulté : 
 (4 / 5 ouvrage technique, ou s'adressant à un public averti, ou de vulgarisation scientifique ayant recours à des équations mathématiques (niveau Bac S maximum).)
(4 / 5 ouvrage technique, ou s'adressant à un public averti, ou de vulgarisation scientifique ayant recours à des équations mathématiques (niveau Bac S maximum).)
Jean-Pierre Luminet fait toute la lumière sur les trous noirs !
Un ouvrage accessible et détaillé sur ces fascinants objets, dont même la lumière ne peut s’échapper, par l’un des meilleurs spécialistes mondiaux qui a en outre été le premier a proposer une « image » scientifique de ces objets.
Si vous ne connaissez les trous noirs qu’à travers la représentation qu’en donne le film « Interstellar » (très bon au demeurant), alors ce livre vous réservera quelques (bonnes) surprises et vous permettra d’approfondir toutes les notions que nous n’avons fait ici que survoler…
Une merveille de vulgarisation intelligente, à mettre entre toutes les mains.

Voyage au coeur d’un trou noir (Youtube)
Alain Riazuelo
Alain Riazuelo, astrophysicien à l’IAP et grand spécialiste des trous noirs, nous entraîne avec une grande rigueur scientifique dans une plongée fascinante au cœur de ces objets mystérieux.
Une véritable leçon de science accessible à tous, et merveilleusement mise en images !
Mentionnons bien sûr les articles publiés par la collaboration EHT dans Astrophysical Journal, relatifs à l’ensemble des aspects de ce projet et de l’image obtenue :
First M87 Event Horizon Telescope Results
The Event Horizon Telescope Collaboration et al.
ApJL 875 L1 (10 avril 2019)
I. The Shadow of the Supermassive Black Hole
https://doi.org/10.3847/2041-8213/ab0ec7
II. Array and Instrumentation
https://doi.org/10.3847/2041-8213/ab0c96
III. Data Processing and Calibration
https://doi.org/10.3847/2041-8213/ab0c57
IV. Imaging the Central Supermassive Black Hole
https://doi.org/10.3847/2041-8213/ab0e85
V. Physical Origin of the Asymmetric Ring
https://doi.org/10.3847/2041-8213/ab0f43
VI. The Shadow and Mass of the Central Black Hole
https://doi.org/10.3847/2041-8213/ab1141